El Colegio Laude Fontenebro School (Moralzarzal) diseña sus propias Regletas de Cuisenaire en 3D


Silvia García López, profesora de Infantil, y Luis Zumárraga Sirvent, profesor de Tecnología de Secundaria y Bachillerato, ambos del Colegio Laude Fontenebro School (Morazarzal, Madrid), comparten su experiencia sobre la manipulación de las Regletas de Cuisenaire. ¿Las habéis utilizado vosotros?
Las “regletas” o “números en color” fueron inventadas por Georges Cuisenaire, profesor de la escuela primaria de Bélgica a principios de la década de los años cincuenta del siglo pasado, aunque su uso para la enseñanza de las matemáticas fue desarrollado y popularizado por Caleb Gattegno.
Estamos ante un versátil juego de manipulación matemática que se utiliza para enseñar una amplia variedad de temas como las cuatro operaciones básicas, fracciones, áreas, volumen, raíces cuadradas, resolución de ecuaciones simples, los sistemas de ecuaciones e, incluso, ecuaciones cuadráticas. Es decir, se trata de un material manipulativo a través del cual el alumno va descubriendo conceptos en lugar de que el maestro los muestre o exponga. Al permitir la manipulación de conceptos básicos se favorece la autonomía, la observación y la crítica de los estudiantes.
Índice de contenido:

En el segundo ciclo de Educación Infantil contamos con las regletas como recurso manipulativo a través del cual vamos descubriendo conceptos. Los niños comienzan a familiarizarse y a jugar con ellas desde los 3 años. Además, y en el aula de 5 años, se incorporaron tres nuevos alumnos (uno de ellos ya las conocía y para los otros dos resultó un material nuevo).
Comenzamos la manipulación y comparación de regletas, asociando cada color a un número. A uno de los niños le resultaba muy difícil realizar dicha asociación, por lo que a la hora de realizar cualquier actividad dedicaba mucho tiempo en comprobar qué grafía correspondía con el color de las regletas que manipulaba. Este alumno mostraba gran soltura en la manipulación y experimentación con este material y había ido construyendo por sí mismo conceptos como equivalencias, suma, resta… pero le resultaba muy difícil interiorizar y asociar el color a la grafía. Para ayudarle a interiorizar estas asociaciones, totalmente arbitrarias, colocamos en las paredes del aula, a tamaño grande y en un lugar visible, los números en color. Aun así observamos gran pérdida de tiempo por parte del alumno en comprobar la correspondencia color-grafema.

¿Tendrá este hecho algo que ver con la sinestesia? Es la asimilación conjunta o interferencia de varios tipos de sensaciones de diferentes sentidos en un mismo acto perceptivo. Las personas sinestésicas perciben con frecuencia y de manera involuntaria correspondencias entre tonos de color, tonos de sonidos e intensidades de los sabores. En la sinestesia “grafema en color” una de las formas más comunes que se pueden encontrar es la asociación directa de cualquier signo, letra o número con un color específico.
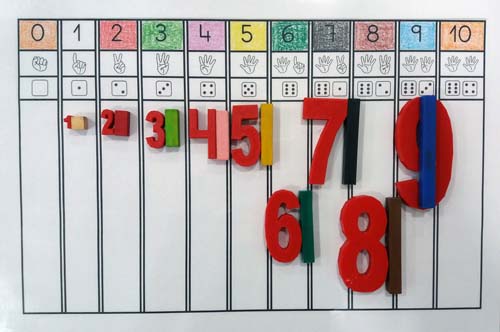
Justo en este momento de reflexión Belén, madre de tres alumnos del Colegio Laude Fontenebro y profesora de Matemáticas en la Universidad de Valladolid, se encontraba experimentando con regletas numéricas en las que se deja a un lado el criterio del color para centrar la atención exclusivamente en el tamaño y longitud de las mismas y la grafía de los números. Estas regletas son todas del mismo color y mantienen una anchura fija, variando la longitud de cada número proporcionalmente a la cantidad correspondiente.
Decidimos llevar al aula estas regletas para probar su funcionalidad, pero antes realizamos ciertas modificaciones, ya que al no variar el ancho de los números la grafía de los mismos se va distorsionando dando lugar a confusiones. Diseñamos y elaboramos nuestras nuevas regletas en 3D. Sin dudar un instante imprimimos en la impresora 3D los primeros diseños.

Con el fin de mantener la proporcionalidad en las grafías, las nuevas regletas numéricas desarrolladas incrementaban la longitud y el ancho de forma proporcional al numeral que representan, de esta forma que se mantenía la legibilidad del número y se podía seguir manipulando de forma proporcional tanto en el eje vertical como en el horizontal. Las dimensiones utilizadas eran coherentes con las regletas de madera, siendo 10 mm de alto y 5 mm de ancho por unidad del numeral representado.
La primera versión la realizamos siguiendo las grafías de los numerales ya disponibles en el programa de dibujo utilizado para el diseño de las regletas. En cuanto estuvieron disponibles comenzamos a trabajar con ellas en el aula y detectamos una serie de fallos de diseño. Por ejemplo, la grafía “inglesa” del número 4 no es la que se enseña en infantil, así que fue necesario modificarla y crear un diseño completamente nuevo del cuatro en grafía “española”. Igualmente ocurría con el 9 y con el número 10 que fue necesario unir el 1 y el 0 para tener un número 10 compacto y manipulable.
Las regletas numerales se han impreso con una impresora 3D en PLA de un sólo color, para desvincular la asociación del color al número, aunque igualmente se podrían imprimir siguiendo el mismo código de colores de Cuisenaire, si se buscase otras aplicaciones didácticas. El set completo de regletas consta de diez “unos”, cinco “doses”, tres “treses”, dos “cuatros” y una unidad del resto de numerales hasta el diez.
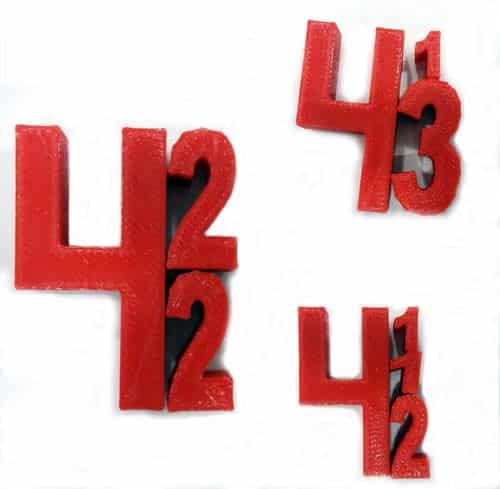
El primer contacto de los niños con las “nuevas regletas” fue mágico. Nada más presentarles el material y preguntarles qué pensaban que podía ser, no dudaron en exclamar “¡Son números regleta!”. No hizo falta explicarles nada. Nos pusimos a experimentar en el aula realizando hipótesis de posibles usos del nuevo recurso y comprobando si eran ciertas o no. Comprobamos que cada número presentado tenía relación con su regleta correspondiente, por lo que nos aventuramos a realizar sumas con los números siguiendo los mismos pasos que seguimos para sumar con las regletas y efectivamente funcionó. Fuimos un poquito más allá y buscamos los números amigos del 2, el 3, el 4 y el 5. Lo que no sabían los niños es que estaban realizando descomposiciones de números, buscando todas las formas posibles de descomposición a la vez que trabajaban la resta, sin llamarlo así.
Desde ese momento todos los niños de la clase tienen a su disposición las Regletas de Cuisenaire y los “números regleta” y ellos mismos eligen qué material utilizar a la hora de realizar operaciones de suma y resta.
1 Comentarios
Muchas felicidades por el trabajo. Me permito invitarte a http://www.oaoamatematicas.org Trabajamos las matemáticas con regletas en todos los niveles